Законы Кеплера являются одними из фундаментальных принципов астрономии. Их сформулировал немецкий астроном Йоханнес Кеплер в 17 веке на основе многолетних наблюдений и математических расчетов. Эти законы описывают движение планет и других небесных тел вокруг Солнца и являются основой для понимания и предсказания их орбитальных характеристик.
Первый закон Кеплера или закон орбит гласит, что планеты движутся по эллиптическим орбитам, в которых Солнце находится в одном из фокусов. Это означает, что расстояние между Солнцем и планетой меняется в течение ее орбиты. Этот закон актуален не только для планет, но и для комет и других небесных тел. Важно отметить, что эллипс достаточно вытянут, и в большинстве случаев выглядит почти как окружность.
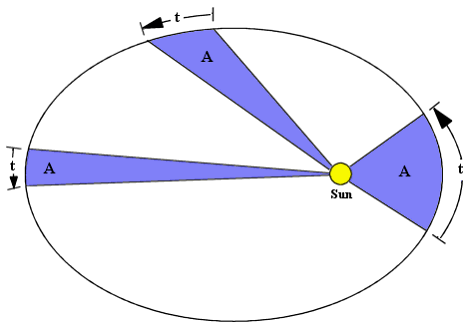
Второй закон Кеплера или закон радиус-вектора устанавливает, что радиус-вектор, проведенный из Солнца к планете, за равные промежутки времени заключает равные площади. Это означает, что планета движется быстрее ближе к Солнцу и медленнее в отдалении от него. Следствием этого закона является тот факт, что планеты находятся ближе к Солнцу при перигелии (наиболее близкой точке орбиты) и дальше при афелии (наиболее удаленной точке орбиты).
Третий закон Кеплера или гармонический закон связывает период обращения планеты вокруг Солнца с ее средним расстоянием до него. Закон утверждает, что квадраты периодов обращения двух планет вокруг Солнца пропорциональны кубам полуосей их орбит. Другими словами, чем дальше от Солнца находится планета, тем дольше ее год (период обращения). Этот закон позволяет установить связь между периодами обращения планет и их расстоянием от Солнца и является основой для определения расстояний в солнечной системе.
В целом, законы Кеплера имеют огромное значение для астрономии и космологии. Они помогают ученым понять движение и эволюцию Солнечной системы, предсказывать положение планет и других небесных тел в определенное время и понять общие закономерности в орбитальном движении. Благодаря этим законам мы можем более глубоко понять устройство Вселенной и ее процессы.
Закон I: Закон эллипса
Этот закон был сформулирован Йоганном Кеплером в начале XVII века на основе наблюдений и математических расчетов. Ранее считалось, что планеты движутся по окружностям, однако Кеплер открыл, что орбиты имеют форму эллипсов.
Важность этого закона состоит в том, что он дал фундаментальное понимание орбитальных движений планет и позволил Кеплеру разработать следующие законы. Закон эллипса также сформулировал основы геометрии орбит и открыл путь к развитию теории гравитации.
| Орбитальные элементы | Описание |
|---|---|
| Эксцентриситет | Мера отклонения эллипса от окружности. Для окружности эксцентриситет равен нулю, для эллипса от 0 до 1. |
| Большая полуось | Половина длины самой длинной оси эллипса. Обозначается символом «a». |
| Фокусное расстояние | Расстояние от центра эллипса до одного из фокусов. Обозначается символом «c». |
Закон эллипса является основополагающим принципом в астрономии и современной космологии. Благодаря ему мы можем более точно описывать и предсказывать движение планет и других небесных тел в Солнечной системе и за её пределами.
Описание и принципы
- Первый закон Кеплера, также известный как закон орбит, утверждает, что планеты движутся вокруг Солнца по эллиптическим орбитам, где Солнце находится в одном из фокусов орбиты. Это отличается от представления античных астрономов о движении планет по круговым орбитам с Землей в центре.
- Второй закон Кеплера, известный как закон радиус-вектора, утверждает, что радиус-вектор, соединяющий Солнце и планету, охваченный за равные промежутки времени, будет один и тот же. Это означает, что планеты перемещаются быстрее в перигелии, ближайшей точке к Солнцу, и медленнее в апогее, самой удаленной точке от Солнца.
- Третий закон Кеплера, известный как закон периодов, связывает длительность года планеты (период ее обращения вокруг Солнца) с ее средним расстоянием от Солнца. Конкретно, квадрат периода обращения планеты пропорционален кубу ее среднего расстояния от Солнца. Этот закон позволяет нам определить временные характеристики орбит планет и сравнивать их с другими планетами в Солнечной системе.
Законы Кеплера являются революционными в своем времени и представляют собой ключевой вклад в развитие астрономии. Они помогли разобраться в движении небесных тел и впервые показали, что Земля не является центром Солнечной системы. Законы Кеплера также были начальными шагами к разработке законов гравитации и общей теории относительности, которые изменили наше понимание о физических процессах во Вселенной.
Результаты и значения
Первый закон Кеплера, или закон орбит, утверждает, что планеты движутся по эллиптическим орбитам вокруг Солнца, где Солнце находится в одном из фокусов орбиты. Этот закон позволяет предсказать форму орбиты и определить, какая планета движется по более круговой орбите, а какая — по более вытянутой.
Второй закон Кеплера, или закон площадей, утверждает, что радиус-вектор, проведенный от Солнца до планеты, за равные промежутки времени заметает равные площади. Это означает, что планеты перемещаются быстрее, когда они ближе к Солнцу, и медленнее, когда они находятся дальше.
Третий закон Кеплера, или закон периодов, связывает период обращения планеты вокруг Солнца с её средним расстоянием от Солнца. Этот закон позволяет определить период обращения планеты и вычислить расстояние между планетами и Солнцем.
Значимость законов Кеплера заключается в том, что они позволяют установить закономерности и регулярности в движении планет, а также предсказывать и объяснять различные астрономические явления. Они являются основой для разработки моделей и теорий о строении и эволюции космоса и имеют важное значение для понимания нашей планеты и вселенной в целом.
Закон II: Закон радиус-вектора
Этот закон был важным шагом в понимании законов движения планет и позволил Кеплеру сформулировать свои законы планетарного движения. Закон радиус-вектора был установлен экспериментально Кеплером на основе наблюдений за планетой Марс.
Суть закона заключается в том, что в разные моменты времени планета движется с различными скоростями по орбите. Ближе к Солнцу (в перигелии) она движется быстрее, а дальше от Солнца (в афелии) медленнее. Когда планета находится в апоцентре орбиты (наибольшее расстояние от Солнца), скорость ее движения минимальна. Как результат, радиус-вектор, перемещаясь по орбите, закрывает одинаковые площади за одинаковые промежутки времени.
Этот закон является первым точным описанием сложного движения планет вокруг Солнца и по сей день остается важным в астрономии. Закон радиус-вектора устанавливает связь между геометрическими характеристиками орбиты планеты и ее движением, что позволяет более глубоко понять законы природы и структуру Солнечной системы.
Описание и принципы
Первый закон Кеплера (закон орбит): Каждая планета движется по эллиптической орбите, в одном из фокусов которой находится Солнце. Этот закон позволяет понять, что планеты не движутся по круговым орбитам, как было предполагалось ранее, а по эллипсам с небольшой эксцентриситетом.
Второй закон Кеплера (закон радиус-векторов): Линия, соединяющая планету и Солнце, сканирует равные площади за равные промежутки времени. Это означает, что планета перемещается быстрее, когда она находится ближе к Солнцу, и медленнее, когда она находится дальше от него. Этот закон указывает на то, что скорость планеты меняется в течение её орбиты.
Третий закон Кеплера (закон периодов): Квадраты периодов обращений планет вокруг Солнца относятся как кубы полуосей их орбит. Другими словами, время, за которое планета совершает оборот вокруг Солнца, зависит от большой полуоси его орбиты. Этот закон позволяет установить связь между периодом обращения планеты и её удалённостью от Солнца.
Законы Кеплера имеют огромное значение, так как они поясняют основные принципы движения планет и устанавливают связь между различными параметрами и характеристиками орбит. Эти законы существенно изменили представление о космосе и послужили толчком для развития физических теорий, включая гравитационную теорию Ньютона и общую теорию относительности Эйнштейна.
Результаты и значения
Изучение законов Кеплера позволило сделать важные открытия в астрономии и сформировать основы современной науки о движении планет и небесных тел. Вот некоторые из главных результатов и значений законов Кеплера:
| Закон Кеплера | Результат и значение |
|---|---|
| Первый закон (Закон орбит) | Показал, что планеты движутся по эллиптическим орбитам вокруг Солнца, что оправдало геоцентрическую модель и привело к гелиоцентрической модели Солнечной системы. |
| Второй закон (Закон радиус-вектора) | Установил связь между скоростью планеты в разных точках орбиты, позволяя лучше понять ее движение и предсказать положение в будущем. Также это привело к пониманию того, что планеты движутся быстрее вблизи Солнца и медленнее на большем расстоянии. |
| Третий закон (Закон гармонических периодов) | Обнаружение связи между периодами обращения планет вокруг Солнца и их расстояниями от него, что дало возможность вычислить расстояние до планет и других небесных объектов. Этот закон также помог понять, что спутники других планет также подчиняются закону гармонических периодов. |
Таким образом, законы Кеплера представляют собой ключевые результаты астрономии, которые дали возможность лучше понять движение планет и других небесных тел. Они являются одними из важнейших принципов в изучении вселенной и оказали огромное влияние на развитие науки в целом.
Закон III: Закон периодов
Согласно Закону периодов, квадраты периодов обращения планет пропорциональны кубам их средних расстояний до Солнца. Другими словами, если обозначить период обращения планеты как T и среднее расстояние до Солнца как R, то имеет место следующая зависимость:
T^2 ∝ R^3
Это означает, что планеты, находящиеся дальше от Солнца, имеют более длительные периоды обращения. Например, Земля обращается вокруг Солнца за примерно 365 дней (один год), в то время как Марс – за около 687 дней.
Открытие и формулировка данного закона Кеплером позволили более точно определить средние расстояния до Солнца для различных планет. Закон периодов стал одним из основных инструментов для изучения и классификации планетарных систем.
Закон периодов также имеет важное значение для определения массы звезды, вокруг которой обращается планета. Изучение изменений периода обращения позволяет астрономам определить, насколько масса планеты влияет на движение планетарной системы в целом.
Основанный на наблюдениях и математическом анализе, Закон периодов является одним из ключевых принципов астрономии, который помогает понять и объяснить движение планет и других небесных тел в Солнечной системе и за её пределами.
Описание и принципы
Первый закон Кеплера, известный как закон орбит, гласит, что все планеты движутся по эллипсам с Солнцем в одном из фокусов. Этот закон позволил установить, что орбиты планет не являются окружностями, как считалось ранее, а имеют эллиптическую форму.
Второй закон Кеплера, называемый законом радиус-вектора, утверждает, что радиус-вектор, соединяющий планету и Солнце, заметает равные площади за равные промежутки времени. Это означает, что скорость планеты в разных точках орбиты меняется, при этом её скорость всегда пропорциональна сектору площади между радиус-вектором и касательной к орбите в данной точке.
Третий закон Кеплера, известный как гармонический закон, устанавливает связь между периодом обращения планеты вокруг Солнца и её средним расстоянием до Солнца. Согласно данному закону, квадрат периода обращения планеты пропорционален кубу полуоси её орбиты.
Законы Кеплера оказали огромное влияние на развитие астрономии и стали основой для формулирования гравитационного закона Ньютона. Они дали возможность более точно описывать движение планет и способствовали созданию модели Солнечной системы, при которой Солнце оказалось в центре и планеты движутся вокруг него. Эти законы имеют важное значение в понимании природы движения планет и до сих пор актуальны в астрономических исследованиях.
Вопрос-ответ:
Какие основные принципы лежат в основе законов Кеплера?
Основные принципы законов Кеплера в астрономии включают следующее: первый закон Кеплера (закон планетарных орбит) гласит, что планеты движутся по эллиптическим орбитам с Солнцем в одном из фокусов; второй закон Кеплера (закон равных площадей) предписывает, что за равные промежутки времени планеты обходят равные площади на своих орбитах; третий закон Кеплера (закон гармонии) устанавливает зависимость между периодами обращения планет вокруг Солнца и их удаленностями от Солнца.
Какова значимость законов Кеплера в астрономии?
Законы Кеплера имеют огромную значимость для астрономии. Они позволяют понять и описывать движение планеты вокруг Солнца, а также предсказывать исходящие из этого движения явления, такие как смена сезонов, фазы Луны и т.д. Благодаря законам Кеплера мы можем определить форму и размеры орбит планет, а также понять, как планеты расположены относительно Солнца и друг друга. Эти законы стали фундаментальными в астрономии и способствуют развитию науки о Вселенной.
Как можно доказать первый закон Кеплера?
Первый закон Кеплера можно доказать, изучая движение планет на небесной сфере. Планеты наблюдаются с Земли и их позиции регистрируются с течением времени. Анализ этих позиций позволяет установить, что планеты движутся по орбитам, близким к эллиптическим, и что Солнце находится в одном из фокусов этих эллипсов. Другой способ — использование космических телескопов, которые наблюдают планеты непосредственно и подтверждают, что их траектории соответствуют первому закону Кеплера.
Какие законы Кеплера существуют?
В астрономии существуют три закона Кеплера: первый закон (закон орбит), второй закон (закон радиус-вектора) и третий закон (закон гармонии).
Что гласит первый закон Кеплера?
Первый закон Кеплера гласит, что планеты движутся по эллиптическим орбитам вокруг Солнца, где Солнце находится в одном из фокусов овала.
Каково значение второго закона Кеплера?
Второй закон Кеплера гласит, что радиус-вектор, соединяющий планету и Солнце, за равные промежутки времени сканирует равные площади на плоскости орбиты.
Чем полезен третий закон Кеплера?
Третий закон Кеплера позволяет определить период обращения планеты вокруг Солнца, используя только информацию о её среднем удалении от Солнца. Это важно для понимания структуры и движения планетарных систем.